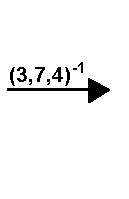15
15 14
14 10
10 6
6 5
5 1
1 2
2 6
6 10
10 14
14 15
15 16
1616
 15
15 11
11 7
7 6
6 2
2 3
3 7
7 11
11 15
15 16
1616
 12
12 8
8 7
7 3
3 4
4 8
8 12
12 16
1616
 15
15 14
14 10
10 9
9 5
5 6
6 10
10 14
14 15
15 16
1616
 15
15 11
11 10
10 6
6 7
7 11
11 15
15 16
1616
 12
12 11
11 7
7 8
8 12
12 16
1616
 15
15 14
14 13
13 9
9 10
10 14
14 15
15 16
1616
 15
15 14
14 10
10 11
11 15
15 16
1616
 15
15 11
11 12
12 16
16
(2,6,3)
(3,7,4)
(5,9,6)
(6,10,7)
(7,11,8)
(9,13,10)
(10,14,11)
(11,15,12)